Μηχανική πρόσθεση
Πρόσθεση σε ευθεία: Ο πίνακας αποτελείται από 3 διαβαθμισμένες γραμμές, όπως στο ggb. Η μεσαία γραμμή έχει κλίμακα με μονάδα δύο φορές μικρότερη από αυτή της πρώτης και της τρίτης γραμμής. Για να πάρουμε το άθροισμα δύο ακεραίων αριθμών σχεδιάζουμε το τμήμα που ενώνει τους δύο αριθμούς και διαβάζουμε απευθείας τη τομή στη μεσαία γραμμή.
Α και Γ Γυμνασίου
Εκτιμάται ότι ο χάρακας αυτός απευθύνεται ιδιαίτερα σε μαθητές με μαθησιακές δυσκολίες.
Θεώρημα: Η τετμημένη μέσου ευθυγράμμου τμήματος ισούται με το ήμισυ του αθροίσματος των τετμημένων των άκρων.
Κατασκευή τετραγωνικής ρίζας
Χαράξτε ένα ημικύκλιο με διάμετρο r +1 (ΑΒ=1, ΒΓ= r), r ένας πραγματικός θετικός αριθμός. Χαράξτε την κάθετο ΒΑ στην ΓΔ.
Τότε ΑΒ^2=ΓΒ*ΒΔ ή ΑΒ^2= r*1= r.
Το τμήμα ΑΒ έχει μήκος ίσο με τη τετραγωνική ρίζα του αριθμού n.
Εκτιμάται ότι η κατασκευή αυτή απευθύνεται και σε μαθητές με μαθησιακές δυσκολίες.
Για Γ Γυμνασίου & Β Λυκείου
Το σπίτι του Descartes στο Amsterdam, 60 Westermart, στο ίδιο τετράγωνο με το σπίτι της Anne Frank.
O Descartes χρησιμοποίησε κανόνα και διαβήτη για να κατασκευάσει αλγεβρικούς αριθμούς.
Κατασκευή κυβικής ρίζας
Η κυβική ρίζα ενός αριθμού δεν μπορεί να κατασκευασθεί με κανόνα και διαβήτη (όπως η τετραγωνική). Παρ' όλα αυτά είναι δυνατόν να δώσουμε μια κατασκευή με τα Συστήματα Δυναμικής Γεωμετρίας.
Ας υποθέσουμε ότι θέλουμε να κατασκευάσουμε τη κυβική ρίζα του αριθμού θετικού s.
Χαράξτε τις παραβολές y = x^2 και y^2 = s x.
Tότε: x^4 = s x ή x(x^3 - s)=0
Η τομή λοιπόν των δύο παραβολών είναι το σημείο O(0,0) και το σημείο Β με τετμημένη ίση με τη κυβική ρίζα του s.
Εκτιμάται ότι η κατασκευή αυτή απαευθύνεται και σε μαθητές με μαθησιακές δυσκολίες.
Για Γ Γυμνασίου & Β Λυκείου
Κατασκευή καθέτου σε σημείο ευθείας με κανόνα και διαβήτη
Δίδονται μια ευθεία (ε) και ένα σημείο Μ πάνω στην ευθεία. Θέλουμε να χαράξουμε μια κάθετο στην ευθεία (ε) από το σημείο Μ. Έχουμε στη διάθεσή μας έναν κανόνα (όχι διαβαθμισμένο) και ένα σκουριασμένο διαβήτη ο οποίος ούτε ανοίγει ούτε κλείνει.
O διαβήτης παραμένει ανοικτός σε μια θέση. Με κέντρο το Μ χαράσσω κύκλο
με τον διαβήτη. Με κέντρα τα σημεία Α και Β χαράσσω άλλους δύο
κύκλους οι οποίοι τέμνουν τον κύκλο με κέντρο το Μ στα σημεία Γ, Δ, Ε και Ζ.
Φέρω τα ευθ. τμήματα ΓΒ, ΕΑ και ΑΖ, BΔ. Η ευθεία ΡΤ είναι η ζητούμενη.
Για Γ Γυμνασίου και Α Λυκείου
Κατασκευή παραλλήλου προς ευθεία από σημείο μόνο με διαβήτη
Δίδονται μια ευθεία (ε) και ένα σημείο Μ εκτός της ευθείας. Θέλουμε να χαράξουμε μια παράλληλο (μ) προς την ευθεία από το σημείο Μ. Έχουμε στη διάθεσή μας μόνο έναν διαβήτη.
Με κέντρο το σημείο Μ κατασκευάζουμε έναν κύκλο (Μ,Β) ο οποίος τέμνει
την ευθεία. Με κέντρο το Β κατασκευάζουμε έναν κύκλο (Β,Μ) ίσης ακτίνας
με τον προηγούμενο που τέμνει την ευθεία (ε) στο Γ. Τέλος, κατασκευάζουμε
τον κύκλο (Γ,Β), επίσης της ίδιας ακτίνας με τους προηγούμενους που τέμνει
τον κύκλο (Μ,Β) στο Δ.
Η ευθεία ΜΔ είναι η ζητούμενη. (Γιατί?)
Στο αρχείο του Geogebra, μετακινείστε το σημείο Μ κάτω από την ευθεία (ε).
Θα δείτε ότι η κατασκευή καταστρέφεται. Αυτό οφείλεται αποκλειστικά
στο λογισμικό (γιατί?). Σε άλλο λογισμικό (πχ το JEX) η κατασκευή δεν έχει πρόβλημα.
Για Γ Γυμνασίου και Α Λυκείου
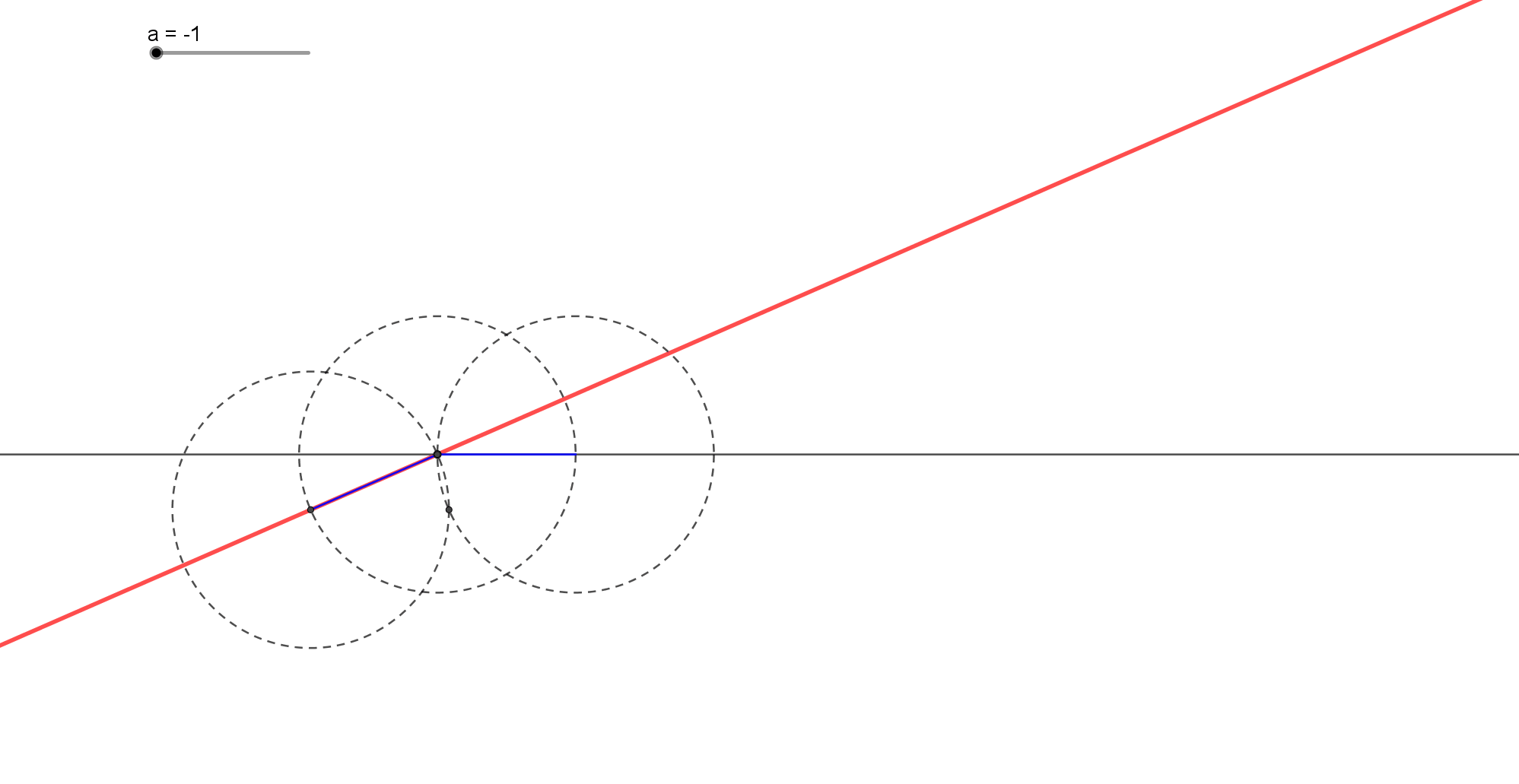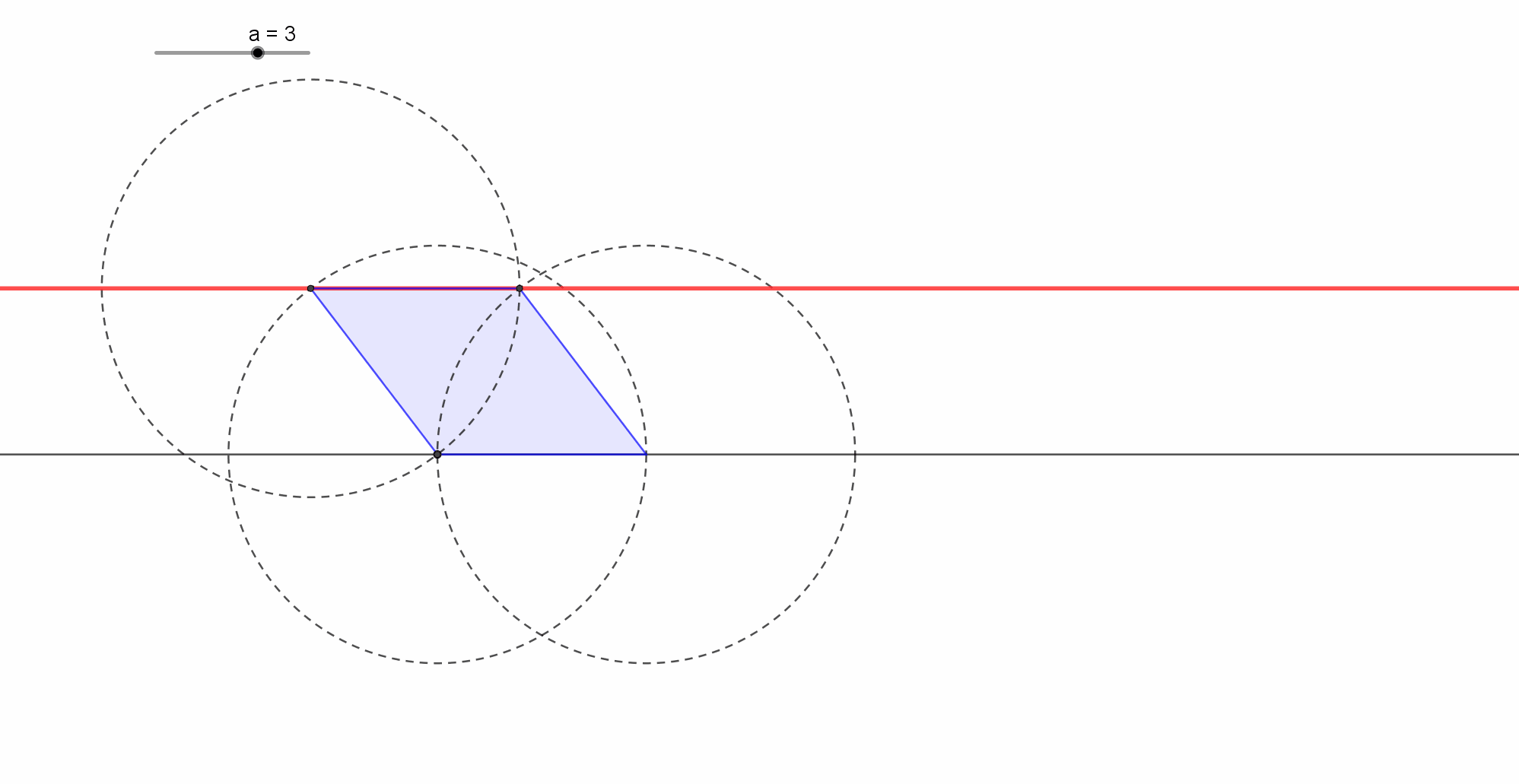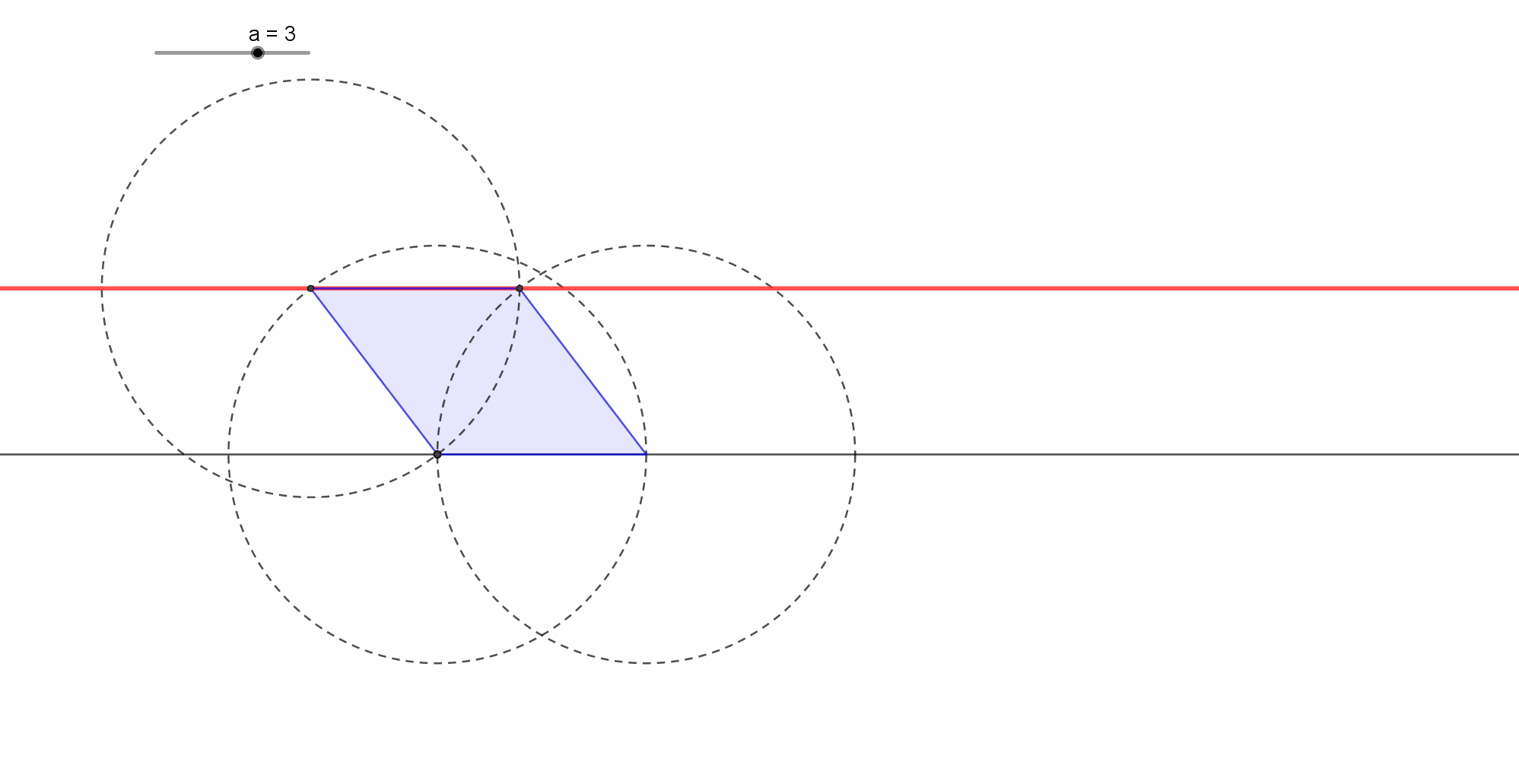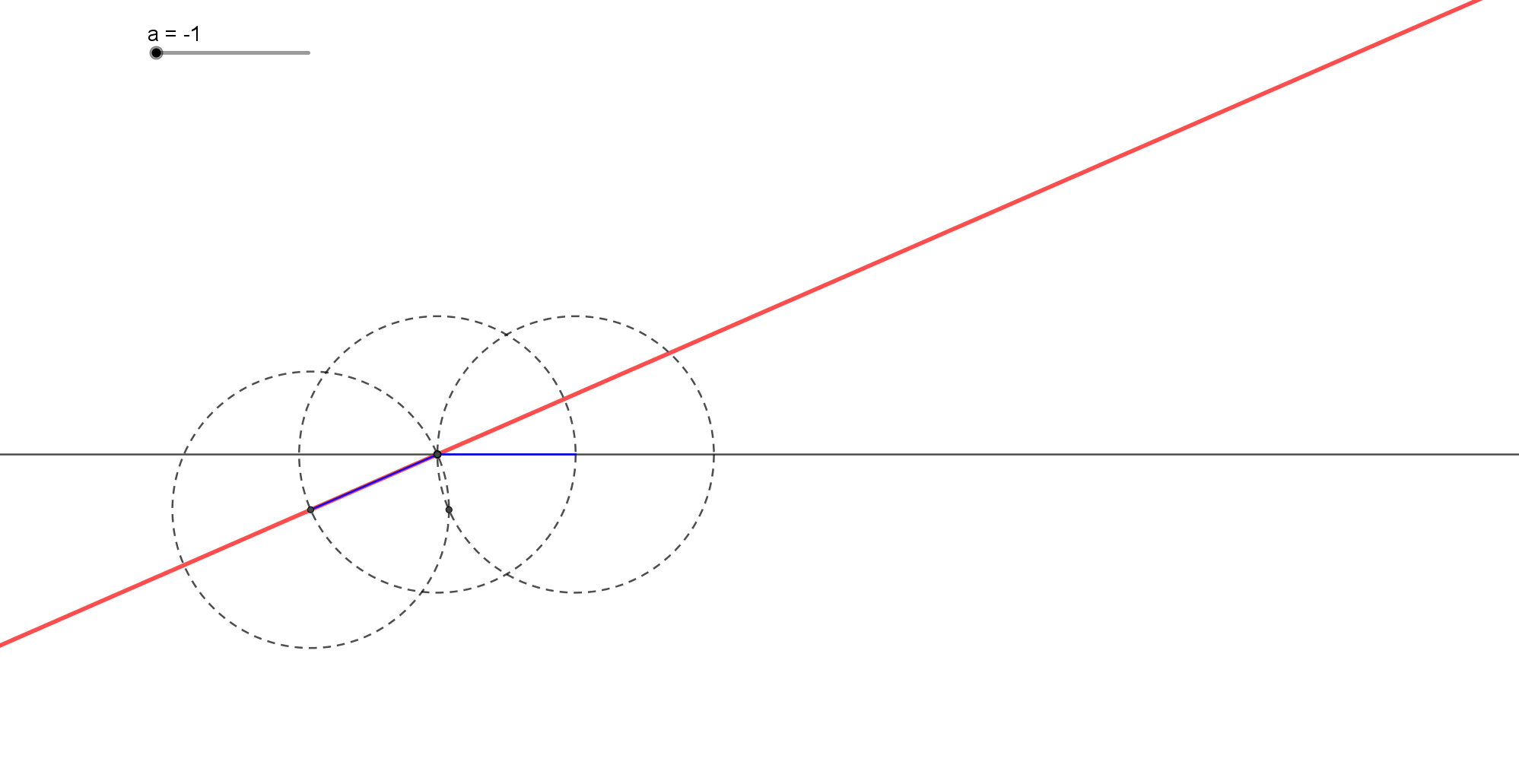
Κατασκευή μέσου ευθ. τμήματος μόνο με χάρακα.
Δίδεται ένα ευθύγραμμο τμήμα ΑΒ και μια ευθεία παράλληλη (ε) προς το ΑΒ. Ζητάμε να κατασκευάσουμε μόνο με τον χάρακα το μέσο Μ του ευθυγράμμου τμήματος Μ.
Από ένα σημείο Δ εκτός του ημιεπιπέδου που σχηματίζει η (ε) και δεν περιέχει το ΑΒ, φέρω τις ευθείες ΑΔ και ΒΔ που τέμνουν την (ε) στα Κ και Λ αντίστοιχα. Αν Ο το σημείο τομής των ΑΛ και ΒΚ, η τομή Μ της ΔΟ και ΑΒ, είναι το ζητούμενο σημείο.
Η απόδειξη θέλει το θεώρημα Θαλή.
Για Γ Γυμνασίου και Α, Β Λυκείου
Κατασκευή άξονα παραβολής με κανόνα και διαβήτη
Μια παραβολή έχει χαραχθεί σε ένα χαρτί. Με τη βοήθεια ενός χάρακα (όχι διαβαθμισμένος) να χαράξετε τον άξονά της.
Έστω Α και Β δύο σημεία της παραβολής (τυχαία). Έστω Γ σημείο διαφορετικό του Α και Β. Φέρω την παράλληλο από το Γ προς την ΑΒ. Έστω Δ το σημείο τομής της παραλλήλου με την παραβολή. Ενώνω τα μέσα Μ και Ν των ΓΔ και ΑΒ. Από το Α φέρω κάθετο στην ΜΝ που τέμνει την παραβολή στο Ε. Ο άξονας της παραβολής είναι τότε η μεσοκάθετος (ε) του ΑE.
Πολλαπλασιασμός Descartes: Προτάθηκε από τον Descartes (1596-1680). Για να πάρουμε το γινόμενο δύο αριθμών (θετικών) που είναι ίσα με τα μήκη των ευθ. τμημάτων ΟB και ΟΓ αντίστοιχα, αρκεί να μετρήσουμε το μήκος του OM. Το μήκος OA = 1.
Α και Γ Γυμνασίου
Εκτιμάται ότι η κατασκευή αυτή απευθύνεται ιδιαίτερα σε μαθητές με μαθησιακές δυσκολίες.
Θεώρημα: Είναι άμεση εφαρμογή του Θεωρήματος Θαλή, αφού AB//ΓΜ, και ΟΜ/ΟΒ=ΟΓ/ΟΑ.
Πολλαπλασιασμός Matiiasevitch: O πολλαπλασιασμός αυτός είναι εμπνευσμένος από το πρόσφατο έργο του Yuri Matiiasevitch και του Boris Stechkin. Για να πάρετε το γινόμενο 2 αριθμών, a και b, μετακινήστε απλά τα σημεία Α και Β - ένα στο κάτω και το άλλο στο πάνω μέρος του γραφήματος της y=x^2 σχετικά με τον άξονα των τετμημένων- έτσι ώστε να πάρουν οι τεμπημένες τους τη θέση των αριθμών a και b. Το γινόμενο a*b διαβάζεται αμέσως στη τομή της ευθείας ΑΒ και του άξονα συμμετρίας της παραβολής. Μπορεί να χρησιμοποιηθεί σε ακεραίους αλλά και μη.
Για να δείτε πως λειτουργεί αυτό το γεωμετρικό κόσκινο, δείτε το αρχείο pdf.
Tο αρχείο ggb ειναι η εφαρμογή.
Γ Γυμνασίου Α και Β Λυκείου
Μέγιστη Περίφραξη
Περίβλημα με πεντόμινα: Ένα πεντόμινο είναι πέμτε τεράγωνα ενωμένα, όπως βλέπετε στο σχήμα
Θέλουμε να χρησιμοποιήσουμε τα παραπάνω 12 πεντόμινα έτσι ώστε να σχηματίσουμε μια περίφραξη με μέγιστο δυνατό εμβαδόν. Αυτό θα γίνει σύμφωνα με 2 αρχές:
1) δύο πεντομίνα βρίσκονται πάντα σε επαφή από τη μία πλευρά των βασικών τετραγώνων.
2) δύο πεντομίνα μπορούν να έρθουν σε επαφή μόνο σε μία κορυφή.
Πηγή: Rodolfo Marcelo Kurchan που αναφέρεται από το περιοδικό Jouer Jeux Mathématiques n°17
Α και Γ Γυμνασίου
Εκτιμάται ότι ο το πρόβλημα απευθύνεται ιδιαίτερα σε μαθητές με μαθησιακές δυσκολίες.
Μέχρι σήμερα έχουμε δύο λύσεις:
1) Donald Knuth (Scientific American, Juin 1973). 2) Vejmola Stan, το εμβαδόν είναι 161 μ^2
Το εμβαδόν του περιφραγμένου χώρου είναι 128μ^2.
Γεωμετρική Πολυπλοκότητα (Lemoine)
Ο Hilbert εξέφρασε για πρώτη φορά την επιθυμία για μέγιστη απλότητα (simplicity) στις μαθηματικές αποδείξεις. Ο Lemoine (1840 – 1912) ήταν από τους πρώτους μαθηματικούς που υιοθέτησαν την άποψη αυτή για τις αποδείξεις στην γεωμετρία.
To 1893, o Lemoine ανήγαγε όλες τις υπάρχουσες γεωμετρικές κατασκευές με κανόνα και διαβήτη σε πέντε πράξεις στη Γεωμετρία. Δημιούργησε ένα σύστημα κατασκευών, τη γεωμετρικογραφία ( geometrography), με τη βοήθεια της οποίας μέτρησε την απλότητα (simplicity) και την πολυπλοκότητα (complexity) του συνολικού αριθμού των πέντε βασικών πράξεων που χρησιμοποιούμε σε μια κατασκευή. Με κάποιο τρόπο θα λέγαμε ότι έδωσε το μέτρο πολυπλοκότητας μιας γεωμετρική κατασκευής. Με κάποιο ανάλογο τρόπο, ο Hilbert ήθελε σε γενικές γραμμές να κάνει την μαθηματική απόδειξη ένα μετρήσιμο αντικείμενο της Αριθμητικής στην οποία μόνο πεπερασμένες (finitism) διαδικασίες ήταν αποδεκτές.
Αν και το άθροισμα των σταθερών του Lemoine που δίνει την απλότητα και την πολυπλοκότητα μιας κατασκευής είναι γεωμετρικό μέγεθος και όχι αριθμητικό, με αποτέλεσμα οι μετρήσεις των κατασκευών να είναι μεταξύ τους μη συγκρίσιμες, η μέτρηση του Lemoine παραμένει μέχρι σήμερα το μόνο συστηματικό μέτρο για να συγκρίνουμε κατασκευές μεταξύ τους. Στο [2] ο Mustonen προτείνει ένα στατιστικό μοντέλο για τη μέτρηση της ακρίβειας μιας κατασκευής. Σήμερα, διαθέτουμε πολύτιμα εργαλεία για να ελαχιστοποιήσουμε το κόστος της καταγραφής των βημάτων, ιδίως στα προβλήματα με σχετικά μεγάλο αριθμό βημάτων. Τα εργαλεία αυτά δεν είναι τίποτα άλλο παρά τα συστήματα δυναμικής γεωμετρίας και αυτοματοποιημένων αποδείξεων, τα οποία πέρα της ευκολίας διαθέτουν και ένα πρωτόκολλο κατασκευής πάρα πολύ χρήσιμο για την έρευνά μας.
Τα αρχεία της εργασίας (Iώ Λυγάτσικα)
Οι παρακάτω κατασκευές είναι από την Ιώ Λυγάτσικα
Η κατασκευή Lemoine (geogebra)
H κατασκευή Πάμφιλου (geogebra)
Η κατασκευή Epstein (geogebra)
Ένα κλασικό πρόβλημα μεγίστου ελαχίστου με περιορισμούς
Είναι γνωστή η κατασκευή σημείου Μ σε ευθεία (ε), τέτοιο ώστε το άθροισμα των αποστάσεων ΜΑ+ΜΒ, από δύο τυχαία σημεία του επιπέδου της ευθείας, Α και Β, να είναι το ελάχιστο δυνατό. Δείτε στο σχολικό βιβλίο (Αργυρόπουλος Η. κ.αλ. Ευκλείδεια Γεωμετρία, Τεύχος Α), Εφαρμογή 4, σελ. 62).
Το πρόβλημα στη πρώτη περίπτωση, που τα σημεία Α και Β βρίσκονται στο ίδιο ημιεπίπεδο που σχηματίζει η ευθεία (ε), έχει ενδιαφέρον, η δεύτερη περίπτωση η κατασκευή είναι προφανής.
Τι θα γινόταν όμως αν κάναμε την εξής ερώτηση:
Να βρεθεί σημείο M πάνω σε ευθεία (ε) έτσι ώστε η απόσταση MA+MB να είναι η ελάχιστη, αν δεν μπορούμε να χαράξουμε εκτός της παρακάτω εικόνας κάποιο βοηθητικό σημείο ή ευθεία!
Η κατασκευή:
Kατασκευές Sangaku
Το sangaku είναι πινακίδες προβλημάτων γεωμετρίας που επινοήθηκαν και εφαρμόστηκαν ευρέως στην Ιαπωνία κατά τη διάρκεια των αιώνων, κυρίως όταν η Ιαπωνία απομονώθηκε από Δυτικές επιρροές, γύρω στο 16ο αιώνα. Η γεωμετρία στην Ιαπωνία είναι ένα μίγμα τέχνης και μαθηματικών.
Τα sangaku, είναι ξύλινες πινακίδες, κάτι σαν tablet εποχής, με ζωγραφισμένα γεωμετρικά και αριθμητικά στοιχεία και φυλασσόταν συνήθως στους βουδιστικούς ναούς ή στα ιερά Sinhto. Κάθε πινάκιο δηλώνει ένα θεώρημα ή πρόβλημα. Είναι ένας τροπος επικοινωνίας των μαθηματικών ώστε να κοινοποιήσουν την εκφώνηση καθώς και την επισυναπτόμενη απόδειξη ενός θεωρήματος ή την λύση ενός προβλήματος.
Τα sangaku είναι φθαρτά, και η πλειοψηφία τους έχει αποσυντεθεί και εξαφανιστεί κατά τη διάρκεια των δύο τελευταίων αιώνων, αρκετά όμως από αυτά έχουν διασωθεί μέχρι σήμερα.
Στην Ελλάδα για πρώτη φορά παρουσιάστηκαν τα προβλήματα αυτά στο τεύχος 4 του Απολλώνιου, περιοδική έκδοση της ΕΜΕ Ημαθίας, από τον Γιάννη Απλακίδη το 2004.
Κατασκευή Χρυσής Τομής
Η χρυσή τομή είναι είναι μια κατασκευή που χωρίζει ένα δοθέν ευθύγραμμο τμήμα σε δύο μέρη που λέμε ότι έχουν την χρυσή αναλογία. Αν a και b (a>b) είναι αυτά τα δύο τμήματα τότε: a/b=(a+b)/a=φ.
Δίνουμε τέσσερις κατασκευές της χρυσής τομής, 3 ακριβής και μια με προσέγγιση. Δείτε το παρακάτω επισυναπτόμενο:
Πρόβλημα
Να ξανακατασκευάσετε το παρακάτω σχήμα έως το 10ο τετράγωνο. Αν η πλευρά του μεγάλου τετραγώνου είναι 24cm,να βρεθεί το εμβαδόν του 10ου τετραγώνου.
Μια υπόδειξη:
Εγγραφή κανονικών πολυγώνων
Υπάρχει ένας ισχυρισμός στα μαθηματικά που ονομάζεται Ισχυρισμός του Toeblitz που λέει ότι:
Σε κάθε καμπύλη Jordan υπάρχουν τέσσερα σημεία που είναι κορυφές τετραγώνου.
Μια καμπύλη Jordan είναι μια απλή κλειστή καμπύλη στο πραγματικό επίπεδο. Προφανώς δεν θα μιλήσουμε για το πρόβλημα αυτό εδώ. Με αφορμή όμως του ισχυρισμού του Toeblitz θα δούμε τρία προβλήματα που σχετίζονται με την εγγραφή κανονικών πολυγώνων σε σχήματα ξεκινώντας από δύο προβλήματα του βιβλίου του G. Lemaire (Méthodes de resolution et de discussion des problèmes de Géométrie), και χρησιμοποιούν τη στροφή σαν κύρια μεθοδολογία.
Στο δεύτερο πρόβλημα, (εγγραφή τετραγώνου σε παραλληλόγραμμο), ο Lemaire θέτει το ερώτημα της διερεύνησης του πότε μια κορυφή του τετραγώνου μπορεί να παραμείνει στο εσωτερικό μιας πλευράς του παραλληλογράμμου. Δεν είναι εύκολη ερώτηση και θέλει φαντασία στην επιλογή της προσεγγιστικής διαδικασίας.
Ta προβλήματα είναι τα εξής:
-
(Lemaire) Na εγγράψετε ισόπλευρο τρίγωνο ανάμεσα σε τρείς παράλληλες ευθείες.
-
(Lemaire) Να εγγραφεί τετράγωνο σε παραλληλόγραμμο.
-
(Gelca, Razvan, Andreescu, Titu) Να εγγραφεί ισόπλευρο τρίγωνο και τετράγωνο σε έλλειψη.
